Wstęp
Teraz skupimy się na nieco trudniejszym zagadnieniu, czyli poruszaniu się w przestrzeni. Jeżeli jeszcze nie czytałeś/czytałaś części pierwszej, to koniecznie to teraz zrób, ponieważ będę się odwoływał do tego, co już się w niej nauczyliśmy :P
Wektory i ich składanie
Brrrr, wektory - to brzmi strasznie ! Spokojnie, będzie łatwo i przyjemnie - obiecuję !
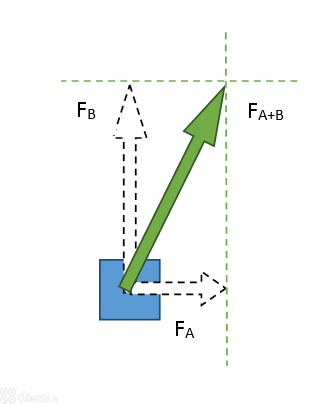
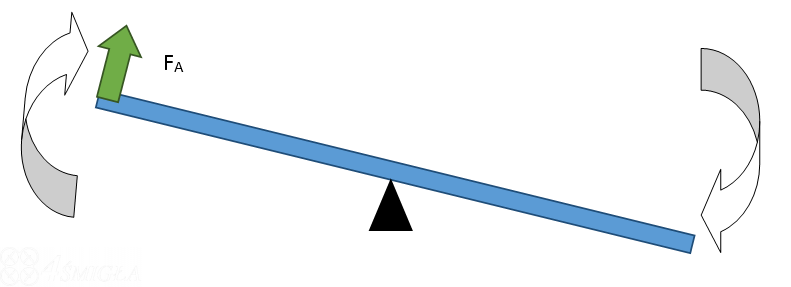
Jak już wiemy, na rysunkach wektory przedstawiamy w postaci strzałki. W przypadku sił, bo o nich wciąż będziemy tutaj mówić, długość strzałki określa wartość - im dłuższa, tym większa siła. Kierunek i zwrot jej działania pokazuje ułożenie strzałki. W przypadku mowy o tzw. składaniu wektorów sprawa z pozoru trudna okazuje się bardzo prosta. Otóż wyobraźmy sobie siłę, która działa tak jak na rysunku poniżej.
Działa ona głównie "w górę" i trochę "w prawo" - zgadza się ? Możemy swobodnie rozbić ją właśnie w ten sposób jak powiedziałem i efekt będzie dokładnie ten sam. Jedna siła działająca po skosie, jak na obrazku może być zamieniona na 2. Jedna działa w pionie (FB), druga w poziomie (FA). Razem dają wypadkową, czyli właśnie naszą wspomnianą wcześniej siłę działającą pod lekkim skosem. Znacie może figurę zwaną trójkątem prostokątnym ? Tak ? To super ! W takim razie, siła będąca wypadkową znajdzie się na przeciwprostokątnej, a siły składowe (te które w wyniku ją tworzą), będą na przyprostokątnych. Zaraz Wam wytłumaczę po co to wszystko.
Lecimy w przód
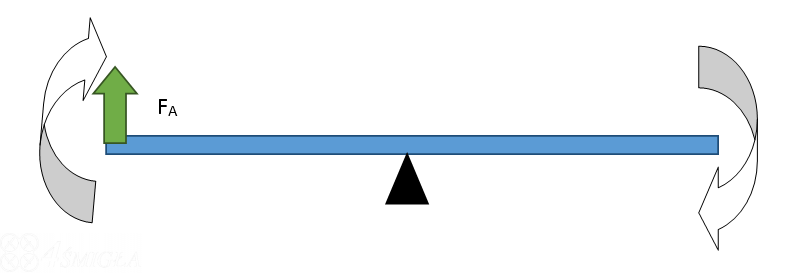
Dotychczas dyskutowaliśmy wyłącznie o utrzymywaniu się w powietrzu i o równowadze, w jakiej pozostaje moc każdego z silników. Teraz wprowadzamy pewną asymetrię. Wróćmy do przykładu naszego kija, na który zadziałamy siłą, ale tylko z jednej strony. Spowoduje to jego obrót, ponieważ z drugiej strony nie ma równoważącej siły.
Uzbrojeni w tą wiedzę możemy teraz pójść o krok dalej i wrócić do naszego unoszącego się w powietrzu kijka. Działa na niego grawitacja, która ciągnie go w dół. Jednocześnie działa on taką samą siłą, ale o przeciwnym zwrocie (w górę), aby utrzymywać się w jednej pozycji. Jeśli teraz z tyłu zastosujemy siłę, która jest większa, niż tylko ta, która kompensuje grawitację (FA > FG1), to tylna część spowoduje obracanie się naszej bryły.
Wypadkowa siła po usunięciu tych, które się znoszą (FB i FG2) będzie więc wyglądać tak, jak na jednej z wcześniejszych ilustracji. Siła FA jest pomniejszona o przeciwstawiającą jej się wartość FG1, dlatego strzałka jest krótsza.
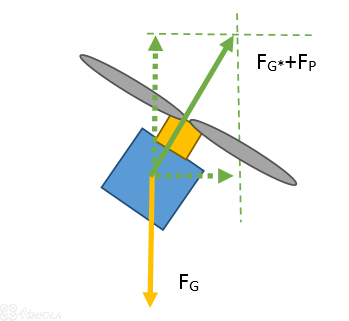
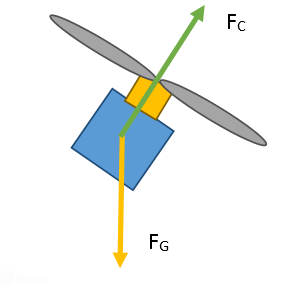
Wprowadzając asymetrię spowodowaliśmy obrót naszej bryły. Od tego momentu siła, która dotychczas ciągnęła nas w górę, teraz działa po skosie. Grawitacja jednak pozostaje bez zmian i działa dokładnie tak samo, jak działała. Zobaczmy teraz, jak to wygląda z perspektywy każdego z ramion osobno. Siła FG działa wciąż w dół. Z kolei śmigło wraz z silnikiem są już pochylone pod kątem, a z racji tego, że siła nośna zawsze jest prostopadła do płatów śmigła - jest ona pochylona dokładnie w ten sam sposób.
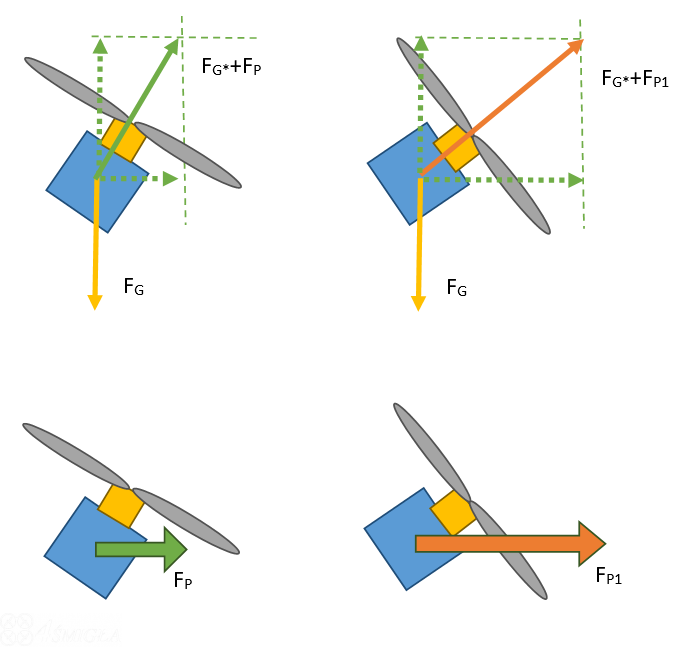
Siłę FG można rozłożyć na składowe, w taki sposób, jak zrobiliśmy to na początku wpisu. Wektor traktujemy jako przeciwprostokątną, zaś boki są składowymi. Strzałki, które zostały narysowane linią przerywaną są więc alternatywnym sposobem przedstawienia siły FG. Zauważmy teraz pewną rzecz. Część siły, która idzie w pionie, nazwiemy FG* - nieprzypadkowo, ponieważ jest ona przeciwstawna do FG. Pozostaje jeszcze Fp, czyli składowa pozioma. Zobaczmy, jak wygląda to na rysunku.
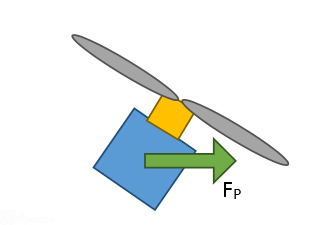
Jak pamiętamy z poprzedniej części, siły FG i FG* w tym przypadku się znoszą. Zostaje nam więc tylko siła Fp, czyli ta, która ciągnie silnik w przód.
Jeżeli teraz przyłożymy sobie wektory sił na każdym z silników do naszej ramy, uzyskamy dokładnie to samo, co działo się w przypadku wcześniejszym. Rama quadrocoptera będzie się poruszać w przód jednocześnie utrzymując stały pułap poprzez równoważenie siły, która ciągnie ramę w dół.
Potrzebujemy jeszcze zrozumieć teorię, która stoi za prędkością lotu w danym kierunku. Otóż wynika ona ze stopnia pochylenia. Zauważmy, że siła FG* musi pozostawać stała, czyli wyrównywać siłę grawitacji, aby kopter nie opadał. Przy coraz większym pochyleniu, nasza przeciwprostokątna musi być coraz dłuższa, aby bok FG* pozostawał stałej długości. Wraz z pochyleniem rośnie jednak składowa pozioma, czyli siła, która ciągnie kopter w przód. Im większe pochylenie, tym większa prędkość lotu, ale też tym szybciej musi się kręcić śmigło, aby wytworzyć odpowiednią siłę nośną.
Powyższy rysunek wyjaśnia dlaczego im bardziej pochylony jest quadrocopter, tym więcej ciągu (gazu) jest potrzebne, żeby utrzymał on ten sam pułap. Teraz już rozumiecie z jakiej przyczyny drogie modele mają silniki bezszczotkowe, posiadające dużo większą moc. Tym samym umożliwiają też dużo szybsze latanie.
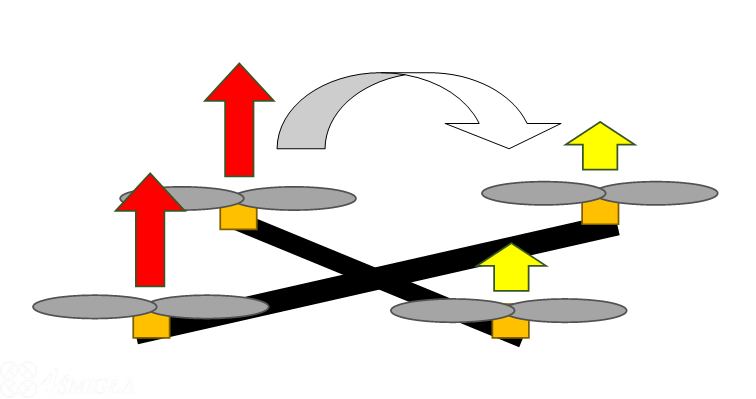
Po omówieniu naszego uproszczonego dwusilnikowego modelu, przejdźmy teraz szybko do tego jak właściwie wygląda praca silników w quadrocopterze. Mówiliśmy już sobie, że ramiona są rozłożone symetrycznie, a więc każdy z silników utrzymuje w powietrzu swoją 1/4 quadrocoptera. Wymuszanie ruchu jest identyczne, jak w przypadku naszego uproszczonego modelu. Jeżeli kopter ma się pochylić w przód, tył, lub na bok, dwa z silników będą pracowały mocniej - one nadadzą rotację, natomiast dwa pozostałe nieco słabiej, aby utrzymać stały pułap i spowodować, że obrót zostanie wykonany bez większego przemieszczenia w poziomie. Na poniższym rysunku widzimy wychylenie koptera w prawą stronę. Lewe silniki pracują mocniej, aby podobnie jak w dwuwymiarowym modelu, wprowadzić lewą stronę w obrót, zaś silniki po prawej, zmniejszają nieco ciąg.
Gdybyśmy chcieli pochylić kopter w przód, dwa tylne silniki pracowałyby szybciej, a dwa przednie - zwolniły nieco obroty.
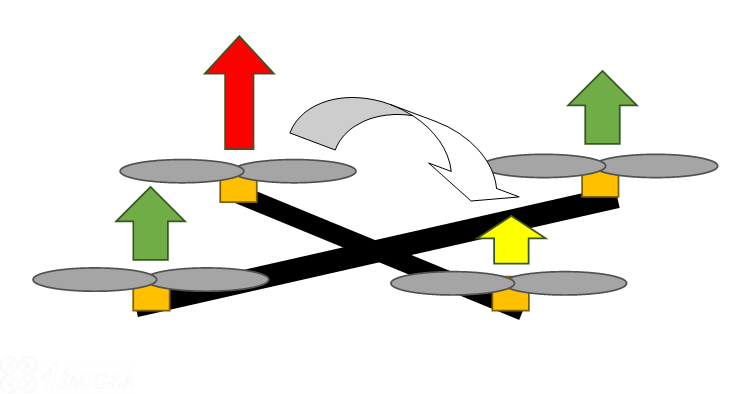
Pozostaje jeszcze kwestia przewrotu po skosie, czyli wzdłuż jednej z osi ramion. Jest to jednocześnie sytuacja pochylenia i wychylenia. Na rysunku poniżej widać przewrót przez prawe tylne ramię. Aby do niego doprowadzić, dwa silniki na lewym tylnym i prawym przednim ramieniu pracują tak, jak zwykle. To wzdłuż tej osi będzie wykonywany obrót. Dwa pozostałe silniki zadziałają tak, jak w przypadku naszego uproszczonego, płaskiego modelu. Lewy przedni przyspieszy nadając ruch obrotowy, a prawy tylny zwolni, aby zmniejszyć siłę nośną po stronie swojego ramienia. W rezultacie uzyskamy obrót taki, jak na obrazku poniżej.
Każdy inny kąt pochylenia będzie wypadał gdzieś pośrednio pomiędzy wskazanymi sposobami pracy silników.
I myślę, że na jeden dzień wystarczy. Ostatnia część będzie opowiadała o tym, w jaki sposób nasz kopter wykonuje obrót w osi pionowej (yaw), w której wykorzystuje on do tego trzecią zasadę dynamiki Newtona. I powiedzcie mi teraz, że fizyka nie jest potrzebna! :)
Póki co zaprzyjaźnijcie się z wektorami i udanych lotów!